课题:立体几何专项复习(第二课时)
上海市第十中学 王涛
一、单元内容分析
1. 单元简介
本单元“立体几何”出自上海教育出版社《数学》必修第三册第10章——空间直线与平面,第11章——简单几何体。本单元包括平面及其基本性质,空间中直线与直线、直线与平面、平面与平面的位置关系,柱体、锥体和球的基本性质及其体积与表面积,旋转体和多面体的概念与性质等。
2. 单元目标
通过本单元的学习,帮助学生从实际情境出发逐步形成空间概念,引出三维空间的基本图形与关系,用数学化的文字语言与符号语言对空间图形及其关系进行自然的描述与论证,以及将空间问题化归为平面问题,在此基础上,帮助学生直观理解空间几何体的结构特征,进一步掌握运用平面直观图表示、处理、分析空间图形的方法和技能,运用简单几何体的基本性质与度量关系解决数学问题和实际问题,进而培养学生的几何直观、空间想象及其相关的逻辑推理能力,发展数学核心素养。
3. 单元结构
本单元由两部分构成:分别是“空间直线与平面”和“简单几何体”
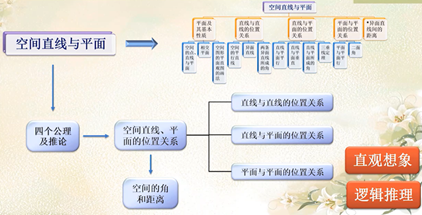

二、教学内容分析
1. 教学内容
本课时为立体几何专项复习的第二课时,教学主要内容有在已学的简单几何体的背景下,综合复习空间直线与平面、平面与平面的位置关系中平行与垂直的判定定理和性质定理,包括定理的数学语言和符号语言的表述,严谨的数学推导过程,以及相应的运用等。
2. 地位作用
本课时中,帮助学生复习用适当的语言与符号准确、简洁地表述立体几何中线面与面面的平行和垂直的判定定理和性质定理,为学生建立空间想象和逻辑推理能力打下基础,初学时会有一定的困难,需要在复习中通过一定数量的训练才能熟练掌握;整个复习过程中,以“线线”“线面”“面面”的位置关系为逻辑主线,由易到难,努力让学生可以构建相对完整的立体几何逻辑体系,并在教学中渗透数学公理化的思想,对学生后续学习复杂几何体的几何结构特征和培育空间想象能力奠定基础。
三、学生学情分析
1. 学生的相关学习经验
学生在初中具备了基本的平面几何知识,在新课教授过程中又已经初步学习了“线线”“线面”“面面”的位置关系,以及平行和垂直的判定定理和性质定理,并学习了用数学语言和符号语言进行论述以及严谨的推到论证,并进行了一些简单的运用。
2.学生可能遇到的学习困难
新课教学中的过程中,“线线”“线面”“面面”的位置关系,以及平行和垂直的判定定理和性质定理每一部分的内容相对独立,单独成节,少有综合运用,且未和柱体与椎体等几何体的几何结构相结合,因此学生在综合运用这些定理解决数学问题和实际问题的过程中可能会出现理解问题,以及逻辑推理表述不准确不科学等问题。
四、教学目标
1. 认识并理解直线与平面,平面与平面的各种位置关系,感受平面与空间相互转化的思想;
2. 复习判定定理与性质定理的证明,掌握运用这些定理进行几何说理论证;
3. 借助立体几何的载体提升空间想象能力和逻辑推理能力,激发学习兴趣与学科自信.
五、教学重点和难点
掌握并运用各类定理与公式等解决一些立体几何的推理证明与运算等;
六、教学策略分析
针对教学重难点的突破,力求为学生梳理一条立体几何中通过关于“平行”和“垂直”的判定定理和性质定理综合运用解决问题的逻辑主线,整个例题的编排按“线线”“线面”“面面”这一学生较为接受的逻辑主线进行安排,通过变式训练,层层深入,强化学生对于定理的理解以及运用。
七、教学过程设计
Part 1 知识梳理(见学案)
Part 2 例题举隅
考点3 立体几何问题中关于“平行”“垂直”的判定定理与性质定理的综合运用
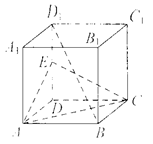
【例题3】如图,在正方体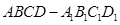 中,
中, 是棱
是棱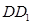 的中点.
的中点.
① 试判断直线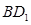 与平面
与平面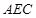 的位置关系,并说明理由; ② 求证:直线
的位置关系,并说明理由; ② 求证:直线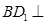 平面
平面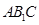 .
.
【变式4】如图,在三棱柱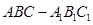 中,每个侧面均为正方形,
中,每个侧面均为正方形,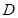 为底面
为底面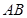 的中点,
的中点, 为侧棱
为侧棱 的中点,
的中点, 与
与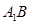 的交点为
的交点为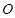 . 求证:①
. 求证:① 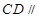 平面
平面 ; ②
; ② 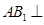 平面
平面 .
.

【变式5】如图,在四棱锥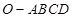 中,底面
中,底面 为平行四边形,
为平行四边形,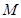 为
为 的中点,
的中点,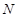 为
为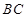 的中点. 求证:
的中点. 求证: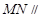 平面
平面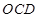 .
.
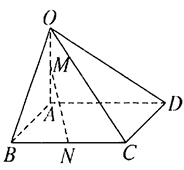
【变式6】如图所示,在四棱锥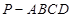 中,底面
中,底面 是矩形,侧棱
是矩形,侧棱 垂直于底面,
垂直于底面, 、
、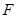 分别是
分别是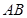 、
、 的中点,
的中点, . 求证:①
. 求证:① 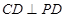 ;②
;② 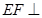 平面
平面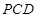 .
.
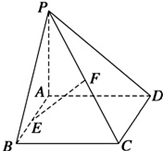
【例题4】如图,四棱锥 中,四边形
中,四边形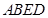 是正方形,若
是正方形,若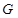 、
、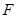 分别是线段
分别是线段 、
、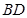 的中点.
的中点.
① 求证: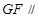 平面
平面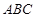 ; ② 在线段
; ② 在线段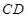 上是否存在一点
上是否存在一点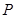 ,使得平面
,使得平面 平面
平面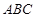 ?并说明理由.
?并说明理由.
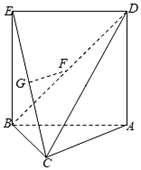
【例题5】如图,已知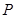 为平面
为平面 外一点,四边形
外一点,四边形 为平行四边形,
为平行四边形,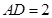 ,
,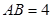 ,
, ,
, ,
, ,
, ,
,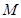 为
为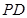 的中点. 求证:平面
的中点. 求证:平面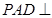 平面
平面 .
.

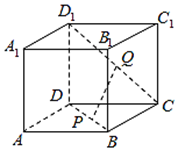
【变式7】如图,在正方体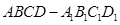 中,
中,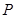 、
、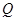 分别为对角线
分别为对角线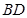 、
、 上的点,且
上的点,且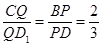 .
.
① 求证: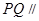 平面
平面 ;
;
② 若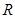 是
是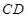 上的点,当
上的点,当 的值为多少时,能使平面
的值为多少时,能使平面 平面
平面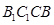 ?请给出证明.
?请给出证明.
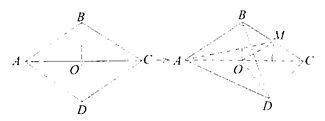
【变式8】如图,菱形 的边长为
的边长为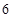 ,
, ,对角线
,对角线 、
、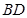 相交于点
相交于点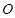 ,将菱形
,将菱形 沿对角线
沿对角线 折起,得到三棱锥
折起,得到三棱锥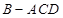 ,点
,点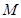 是棱
是棱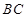 的中点,
的中点,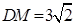 . 求证:①
. 求证:① 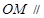 平面
平面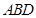 ;② 平面
;② 平面 平面
平面 .
.
Part 3 作业布置:课本50页A组2,4,6,7,8,9题
八、课堂学习评价
以变式8的完成度作为课堂评价载体:
|
评价层级 |
建议评价标准 |
|
第一层级(合格) |
问题(1)解答正确; |
|
第二层级(良好) |
问题(1)解答正确;问题(2)虽未完整解答,但可以根据条件推得线面垂直这一结论,并且可以用规范的数学符号语言进行论述与表达; |
|
第三层级(优秀) |
问题(1)(2)均解答正确,并能用准确规范的数学符号语言进行完整论述; |